图作为一种重要的非线性数据结构,广泛应用于社交网络、路径规划、网络拓扑等领域。图的遍历是图算法的基础,其中深度优先搜索(DFS)和广度优先搜索(BFS)是两种最经典且核心的遍历策略。高效的遍历离不开底层数据结构的支持,即图的存储表示。本文将系统阐述DFS与BFS的原理、特点、应用场景,并深入探讨为其提供支持的几种关键存储服务(邻接矩阵、邻接表等),分析不同存储方式对遍历性能的影响。
一、深度优先搜索(DFS)
深度优先搜索遵循“一条路走到黑,再回溯”的策略。其过程类似于树的先序遍历。
- 核心思想:从起始顶点出发,沿着某条路径尽可能深地探索,直到该路径上所有顶点均被访问,然后回溯到上一个顶点,探索其未访问的其他邻接点,如此反复,直至图中所有从起始点可达的顶点都被访问。
- 实现方式:通常借助栈(递归调用栈或显式栈)来实现回溯功能。递归实现代码简洁,体现了DFS天然的递归结构。
- 算法特点:
- 空间复杂度:在最坏情况下(如图呈线性链状),递归深度为O(|V|),其中|V|为顶点数。
- 时间复杂度:采用邻接表存储时为O(|V|+|E|)(|E|为边数);采用邻接矩阵则为O(|V|²),因为需要遍历整个矩阵来寻找邻接点。
- 生成树/林:DFS遍历过程中经过的边会形成一棵深度优先树(连通图)或多棵深度优先树组成的深度优先森林。
- 典型应用:拓扑排序、寻找连通分量、检测图中是否存在环、求解迷宫问题、寻找图的关节点等。
二、广度优先搜索(BFS)
广度优先搜索遵循“层层推进”的策略,类似于树的层序遍历。
- 核心思想:从起始顶点出发,首先访问其所有邻接点,然后再按访问顺序,依次访问这些邻接点的未被访问的邻接点,以此类推,直到所有可达顶点都被访问。
- 实现方式:必须借助队列来管理待访问的顶点,确保“先被发现的顶点先被访问”。
- 算法特点:
- 空间复杂度:在最坏情况下需要存储一整层的顶点,对于稠密图可能达到O(|V|)。
- 时间复杂度:与DFS相同,邻接表为O(|V|+|E|),邻接矩阵为O(|V|²)。
- 最短路径:在无权图中,BFS从源点出发首次访问到某个顶点的路径,就是该顶点到源点的最短路径。这是BFS一个极其重要的性质。
- 生成树:BFS遍历过程形成的是广度优先树。
- 典型应用:求解无权图的最短路径问题、社交网络中查找“N度好友”、网络广播、GPS导航寻找最少换乘路线等。
三、图的存储支持服务
遍历算法的效率与图的具体存储结构(即“存储支持服务”)紧密相关。主要存储方式有:
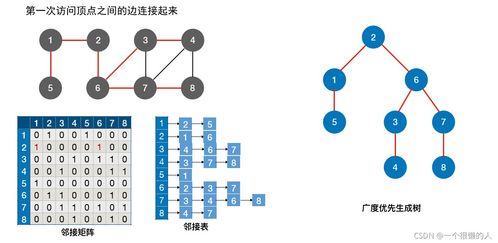
- 邻接矩阵
- 表示方法:使用一个|V|×|V|的二维数组。对于无权图,
matrix[i][j] = 1表示顶点i到j有边,为0则表示无边。对于带权图,可存储权值。
- 遍历支持分析:
- 优点:判断任意两个顶点间是否存在边(即查询操作)非常快,时间复杂度为O(1)。
- 缺点:空间开销大,为O(|V|²),对于稀疏图浪费严重。在遍历时(尤其是BFS/DFS寻找某个顶点的所有邻接点),需要扫描一整行,导致在稀疏图上的遍历效率较低。
- 邻接表
- 表示方法:为每个顶点维护一个链表(或动态数组),链表中存储与该顶点直接相邻的所有顶点(对于带权图,可同时存储权值)。
- 遍历支持分析:
- 优点:空间复杂度为O(|V|+|E|),能高效利用稀疏图的存储空间。在遍历时,能直接获取一个顶点的所有邻接点,无需扫描无效信息,这使得基于邻接表的DFS/BFS时间复杂度优化至O(|V|+|E|)。
- 缺点:判断任意两个顶点间是否有边,需要遍历其中一个顶点的链表,效率为O(度(vertex)),不如邻接矩阵。
- 其他存储结构
- 十字链表:针对有向图的优化存储,结合了邻接表和逆邻接表,方便同时求取顶点的出边和入边。
- 邻接多重表:针对无向图的优化存储,一条边只用一个结点表示,避免了邻接表中边被存储两次的问题,适用于需要频繁操作边的场景。
四、与对比
| 特性 | 深度优先搜索 (DFS) | 广度优先搜索 (BFS) |
| :--- | :--- | :--- |
| 数据结构 | 栈 (递归/显式) | 队列 |
| 遍历顺序 | 深度优先,纵向延伸 | 广度优先,横向扩展 |
| 解的性质 | 不保证最短路径 | 保证无权图最短路径 |
| 空间消耗 | 与递归深度相关,通常较小 | 与每层宽度相关,可能较大 |
| 存储服务影响 | 邻接表效率远高于邻接矩阵 | 邻接表效率远高于邻接矩阵 |
结论:DFS和BFS是图遍历的两大支柱算法,选择取决于问题本身(如求最短路径必用BFS)。而邻接表因其在稀疏图中的空间高效性和遍历时的直接性,成为实现这两种算法最常用、最推荐的“存储支持服务”。在实际系统(如社交网络后端、推荐引擎)中,图的存储服务可能更为复杂,涉及分布式存储、图数据库等,但其核心优化思想依然围绕着如何高效地支持“查找某个顶点的所有邻居”这一遍历基本操作展开。理解基础存储结构与遍历算法的关系,是设计和优化更高级图处理系统的重要基石。