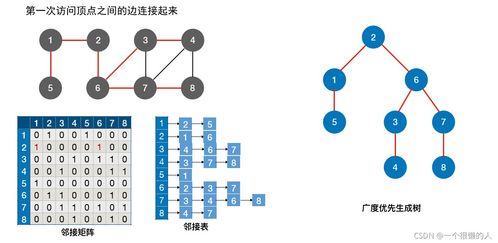
有向无环图表达形式
有向无环图是一种重要的数据结构,广泛应用于计算机科学和工程领域。其核心特点在于图中不存在环路,即从任何一个顶点出发,沿着有向边无法回到该顶点本身。这种结构天然适合表示具有前后依赖关系或顺序约束的场景。常见的表达形式包括邻接矩阵和邻接表。邻接矩阵适用于稠密图,可以快速判断任意两顶点间是否存在边;而邻接表则更节省空间,尤其适合表示稀疏的有向无环图,它能清晰地列出每个顶点的所有后继节点。
拓扑排序:理清依赖顺序
拓扑排序是针对有向无环图的一种线性序列排序算法。它将图中所有顶点排成一个线性序列,使得对于图中的每一条有向边(u, v),在序列中顶点u都出现在顶点v之前。这实质上是将图的结构关系转化为一种可执行的顺序。
算法实现通常采用两种方法:基于深度优先搜索的后序遍历逆序,或基于入度的Kahn算法。后者通过不断移除入度为0的顶点并更新相关顶点的入度来实现排序。拓扑排序在任务调度、课程安排、编译过程中的指令排序等方面有着重要应用,它能有效解决任务间的依赖关系问题。
关键路径:优化项目管理
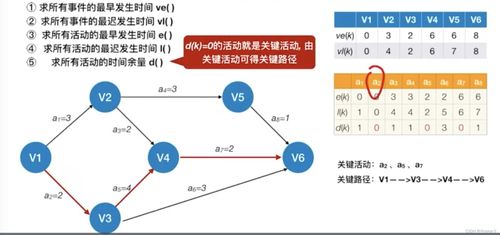
关键路径方法基于有向无环图,专门用于项目计划管理。它通过分析项目中各项活动的持续时间及其依赖关系,确定影响项目总工期的关键活动和路径。图中顶点表示事件(如任务开始或结束),边表示活动,边的权重代表活动持续时间。
关键路径的求解涉及两个核心计算:最早开始时间和最晚开始时间。通过正向计算各事件的最早发生时间,反向计算最晚发生时间,最终确定那些时间余量为零的活动——这些活动构成了项目的关键路径。任何关键活动的延迟都会直接影响项目总工期,因此管理者需要特别关注这些环节的资源分配和进度控制。
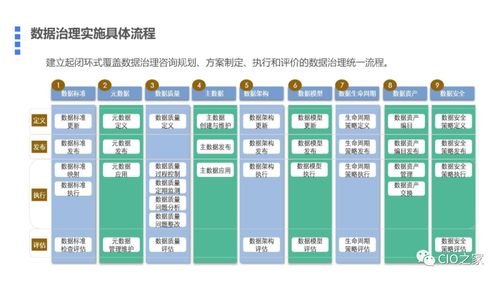
数据处理中的综合应用
在实际数据处理中,有向无环图及其相关算法形成了完整的问题解决框架。从数据依赖分析到执行计划优化,这一系列技术提供了系统化的解决方案。例如,在大数据处理框架如Apache Spark中,有向无环图用于表示数据处理任务之间的依赖关系;在机器学习工作流中,它可用于管理特征工程、模型训练和评估的复杂管道。
将拓扑排序与关键路径分析结合,不仅能确定任务执行顺序,还能识别影响整体处理时间的关键环节,从而实现资源的最优配置和流程的高效执行。这种基于图的数据处理方法,为复杂系统的建模、分析和优化提供了强有力的工具,在现代计算系统中发挥着不可替代的作用。